Rubik's Cube toy puzzle's Invention: 40th Birthday Celebrated With a Google Doodle
Forty years ago today, Erno Rubik, a professor of architecture at the University of Budapest in Hungary created one of the most popular toys of the modern times - the Rubik's Cube. And come its 40th anniversary, Google has celebrated Rubik's Cube invention with an interactive Google doodle in the form of, what else, but a Rubik's Cube.
Like the original version of the popular toy, the Google interactive doodle has a digital version consisting of nine plastic squares of different colours. Users can shift entire rows or columns of the cube to match the squares of the same colours on each individual side.
Google even lets users share the number of moves taken to solve the Rubik's Cube on social networking sites like Facebook and Twitter and also on Google+. Playing the Rubik's Cube invention Google doodle is simple with instructions being as precise as possible for users to understand and play it. A swipe on the outside of the cube allows one to rotate the sides of the cube, while a swipe inside allows to twist and turn the cube to match the colour squares.
Erno Rubik's original cube consisted of a solid cube, which twisted and turned but did not fall apart. Rubik's invention had colourful stickers on the side which got scrambled all over thereby making it the first Rubik's Cube.
While Rubik himself took a while to understand the potential of the toy, ever since its international launch in 1980 the Rubik's Cube has sold over 350 million units worldwide and was also named 'Toy of the Year' in 1980 in Britain. Of course, the simple plastic cube version has now expanded to neon glowing versions, and also into bejewelled versions worth millions.
The first working prototype of the Rubik's Cube was created in 1974 post which it was patented in 1975 as the 'Magic Cube'. It was first sold in Budapest under the name 'Magic Cube' in 1977, and renamed as the Rubik's Cube in 1980.
The first national Rubik's Solving championship was held in 1982. Diamond Cutters Inc. created a diamond version of the cube in 1995. The Rubik's Cube celebrated its 25th anniversary (from the year of it being renamed as the Rubik's Cube in 1980) on 26 July 2005.
Rubik's Cube is a 3-D combination puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 via German businessman Tibor Laczi and Seven Towns founder Tom Kremer, and won the German Game of the Year special award for Best Puzzle that year. As of January 2009, 350 million cubes had been sold worldwide making it the world's top-selling puzzle game.It is widely considered to be the world's best-selling toy.
In a classic Rubik's Cube, each of the six faces is covered by nine stickers, each of one of six solid colours: white, red, blue, orange, green, and yellow. In currently sold models, white is opposite yellow, blue is opposite green, and orange is opposite red, and the red, white and blue are arranged in that order in a clockwise arrangement. On early cubes, the position of the colours varied from cube to cube. An internal pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to consisting of one colour. Similar puzzles have now been produced with various numbers of sides, dimensions, and stickers, not all of them by Rubik.
Although the Rubik's Cube reached its height of mainstream popularity in the 1980s, it is still widely known and used. Many speedcubers continue to practice it and other twisty puzzles and compete for the fastest times in various categories. Since 2003, The World Cube Association, the Rubik's Cube's international governing body, has organized competitions and kept the official world records.
In March 1970, Larry Nichols invented a 2×2×2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together with magnets. Nichols was granted U.S. Patent 3,655,201 on April 11, 1972, two years before Rubik invented his Cube. On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.
In the mid-1970s, Ernő Rubik worked at the Department of Interior Design at the Academy of Applied Arts and Crafts in Budapest. Although it is widely reported that the Cube was built as a teaching tool to help his students understand 3D objects, his actual purpose was solving the structural problem of moving the parts independently without the entire mechanism falling apart. He did not realize that he had created a puzzle until the first time he scrambled his new Cube and then tried to restore it. Rubik obtained Hungarian patent HU170062 for his "Magic Cube" in 1975. Rubik's Cube was first called the Magic Cube (Bűvös kocka) in Hungary. The puzzle had not been patented internationally within a year of the original patent. Patent law then prevented the possibility of an international patent. Ideal wanted at least a recognizable name to trademark; of course, that arrangement put Rubik in the spotlight because the Magic Cube was renamed after its inventor in 1980.
The first test batches of the Magic Cube were produced in late 1977 and released in Budapest toy shops. Magic Cube was held together with interlocking plastic pieces that prevented the puzzle being easily pulled apart, unlike the magnets in Nichols's design. In September 1979, a deal was signed with Ideal to release the Magic Cube worldwide, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many imitations and variations appeared.
Permutations
The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8! (40,320) ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, since an even permutation of the corners implies an even permutation of the edges as well. (When arrangements of centres are also permitted, as described below, the rule is that the combined arrangement of corners, edges, and centres must be an even permutation.) Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 (2,048) possibilities.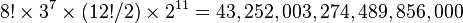
which is approximately 43 quintillion.
The puzzle is often advertised as having only "billions" of positions, as the larger numbers are unfamiliar to many. To put this into perspective, if one had as many standard sized Rubik's Cubes as there are permutations, one could cover the Earth's surface 275 times.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:
which is approximately 519 quintillion possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.
Move notation
Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David Singmaster to denote a sequence of moves, referred to as "Singmaster notation". Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organised on a particular cube.
F (Front): the side currently facing the solver
B (Back): the side opposite the front
U (Up): the side above or on top of the front side
D (Down): the side opposite the top, underneath the Cube
L (Left): the side directly to the left of the front
R (Right): the side directly to the right of the front
ƒ (Front two layers): the side facing the solver and the corresponding middle layer
b (Back two layers): the side opposite the front and the corresponding middle layer
u (Up two layers) : the top side and the corresponding middle layer
d (Down two layers) : the bottom layer and the corresponding middle layer
l (Left two layers) : the side to the left of the front and the corresponding middle layer
r (Right two layers) : the side to the right of the front and the corresponding middle layer
x (rotate): rotate the entire Cube on R
y (rotate): rotate the entire Cube on U
z (rotate): rotate the entire Cube on F
When a prime symbol ( ′ ) follows a letter, it denotes a face turn counter-clockwise, while a letter without a prime symbol denotes a clockwise turn. A letter followed by a 2 (occasionally a superscript 2) denotes two turns, or a 180-degree turn. R is right side clockwise, but R' is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes, corresponding to R, U, and F turns respectively. When x, y or z are primed, it is an indication that the cube must be rotated in the opposite direction. When they are squared, the cube must be rotated 180 degrees.
The most common deviation from Singmaster notation, and in fact the current official standard, is to use "w", for "wide", instead of lowercase letters to represent moves of two layers; thus, a move of Rw is equivalent to one of r.
For methods using middle-layer turns (particularly corners-first methods) there is a generally accepted "MES" extension to the notation where letters M, E, and S denote middle layer turns. It was used e.g. in Marc Waterman's Algorithm.
M (Middle): the layer between L and R, turn direction as L (top-down)
E (Equator): the layer between U and D, turn direction as D (left-right)
S (Standing): the layer between F and B, turn direction as F
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (f b u d l r) refer to the inner portions of the cube (called slices). An asterisk (L*), a number in front of it (2L), or two layers in parenthesis (Ll), means to turn the two layers at the same time (both the inner and the outer left faces) For example: (Rr)' l2 f' means to turn the two rightmost layers counterclockwise, then the left inner layer twice, and then the inner front layer counterclockwise. By extension, for cubes of 6x6 and larger, moves of three layers are notated by the number 3, for example 3L.
An alternative notation, Wolstenholme notation, is designed to make memorizing sequences of moves easier for novices. This notation uses the same letters for faces except it replaces U with T (top), so that all are consonants. The key difference is the use of the vowels O, A and I for clockwise, counterclockwise and 180-degree turns, which results in word-like sequences such as LOTA RATO LATA ROTI (equivalent to LU′R′UL′U′RU2 in Singmaster notation). Addition of a C implies rotation of the entire cube, so ROC is the clockwise rotation of the cube around its right face.
Rubik's Cube software
Puzzles like the Rubik's Cube can be simulated by computer software, which provide functions such as recording of player metrics, storing scrambled Cube positions, conducting online competitions, analyzing of move sequences, and converting between different move notations. Software can also simulate very large puzzles that are impractical to build, such as 100×100×100 and 1,000×1,000×1,000 cubes, as well as virtual puzzles that cannot be physically built, such as 4- and 5-dimensional analogues of the cube.
Forty years ago today, Erno Rubik, a professor of architecture at the University of Budapest in Hungary created one of the most popular toys of the modern times - the Rubik's Cube. And come its 40th anniversary, Google has celebrated Rubik's Cube invention with an interactive Google doodle in the form of, what else, but a Rubik's Cube.
Like the original version of the popular toy, the Google interactive doodle has a digital version consisting of nine plastic squares of different colours. Users can shift entire rows or columns of the cube to match the squares of the same colours on each individual side.
Google even lets users share the number of moves taken to solve the Rubik's Cube on social networking sites like Facebook and Twitter and also on Google+. Playing the Rubik's Cube invention Google doodle is simple with instructions being as precise as possible for users to understand and play it. A swipe on the outside of the cube allows one to rotate the sides of the cube, while a swipe inside allows to twist and turn the cube to match the colour squares.
Erno Rubik's original cube consisted of a solid cube, which twisted and turned but did not fall apart. Rubik's invention had colourful stickers on the side which got scrambled all over thereby making it the first Rubik's Cube.
While Rubik himself took a while to understand the potential of the toy, ever since its international launch in 1980 the Rubik's Cube has sold over 350 million units worldwide and was also named 'Toy of the Year' in 1980 in Britain. Of course, the simple plastic cube version has now expanded to neon glowing versions, and also into bejewelled versions worth millions.
The first working prototype of the Rubik's Cube was created in 1974 post which it was patented in 1975 as the 'Magic Cube'. It was first sold in Budapest under the name 'Magic Cube' in 1977, and renamed as the Rubik's Cube in 1980.
The first national Rubik's Solving championship was held in 1982. Diamond Cutters Inc. created a diamond version of the cube in 1995. The Rubik's Cube celebrated its 25th anniversary (from the year of it being renamed as the Rubik's Cube in 1980) on 26 July 2005.
Rubik's Cube is a 3-D combination puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 via German businessman Tibor Laczi and Seven Towns founder Tom Kremer, and won the German Game of the Year special award for Best Puzzle that year. As of January 2009, 350 million cubes had been sold worldwide making it the world's top-selling puzzle game.It is widely considered to be the world's best-selling toy.
In a classic Rubik's Cube, each of the six faces is covered by nine stickers, each of one of six solid colours: white, red, blue, orange, green, and yellow. In currently sold models, white is opposite yellow, blue is opposite green, and orange is opposite red, and the red, white and blue are arranged in that order in a clockwise arrangement. On early cubes, the position of the colours varied from cube to cube. An internal pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to consisting of one colour. Similar puzzles have now been produced with various numbers of sides, dimensions, and stickers, not all of them by Rubik.
Although the Rubik's Cube reached its height of mainstream popularity in the 1980s, it is still widely known and used. Many speedcubers continue to practice it and other twisty puzzles and compete for the fastest times in various categories. Since 2003, The World Cube Association, the Rubik's Cube's international governing body, has organized competitions and kept the official world records.
In March 1970, Larry Nichols invented a 2×2×2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together with magnets. Nichols was granted U.S. Patent 3,655,201 on April 11, 1972, two years before Rubik invented his Cube. On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.
In the mid-1970s, Ernő Rubik worked at the Department of Interior Design at the Academy of Applied Arts and Crafts in Budapest. Although it is widely reported that the Cube was built as a teaching tool to help his students understand 3D objects, his actual purpose was solving the structural problem of moving the parts independently without the entire mechanism falling apart. He did not realize that he had created a puzzle until the first time he scrambled his new Cube and then tried to restore it. Rubik obtained Hungarian patent HU170062 for his "Magic Cube" in 1975. Rubik's Cube was first called the Magic Cube (Bűvös kocka) in Hungary. The puzzle had not been patented internationally within a year of the original patent. Patent law then prevented the possibility of an international patent. Ideal wanted at least a recognizable name to trademark; of course, that arrangement put Rubik in the spotlight because the Magic Cube was renamed after its inventor in 1980.
The first test batches of the Magic Cube were produced in late 1977 and released in Budapest toy shops. Magic Cube was held together with interlocking plastic pieces that prevented the puzzle being easily pulled apart, unlike the magnets in Nichols's design. In September 1979, a deal was signed with Ideal to release the Magic Cube worldwide, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many imitations and variations appeared.
Permutations
The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8! (40,320) ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, since an even permutation of the corners implies an even permutation of the edges as well. (When arrangements of centres are also permitted, as described below, the rule is that the combined arrangement of corners, edges, and centres must be an even permutation.) Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 (2,048) possibilities.
which is approximately 43 quintillion.
The puzzle is often advertised as having only "billions" of positions, as the larger numbers are unfamiliar to many. To put this into perspective, if one had as many standard sized Rubik's Cubes as there are permutations, one could cover the Earth's surface 275 times.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:
which is approximately 519 quintillion possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.
Move notation
Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David Singmaster to denote a sequence of moves, referred to as "Singmaster notation". Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organised on a particular cube.
F (Front): the side currently facing the solver
B (Back): the side opposite the front
U (Up): the side above or on top of the front side
D (Down): the side opposite the top, underneath the Cube
L (Left): the side directly to the left of the front
R (Right): the side directly to the right of the front
ƒ (Front two layers): the side facing the solver and the corresponding middle layer
b (Back two layers): the side opposite the front and the corresponding middle layer
u (Up two layers) : the top side and the corresponding middle layer
d (Down two layers) : the bottom layer and the corresponding middle layer
l (Left two layers) : the side to the left of the front and the corresponding middle layer
r (Right two layers) : the side to the right of the front and the corresponding middle layer
x (rotate): rotate the entire Cube on R
y (rotate): rotate the entire Cube on U
z (rotate): rotate the entire Cube on F
When a prime symbol ( ′ ) follows a letter, it denotes a face turn counter-clockwise, while a letter without a prime symbol denotes a clockwise turn. A letter followed by a 2 (occasionally a superscript 2) denotes two turns, or a 180-degree turn. R is right side clockwise, but R' is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes, corresponding to R, U, and F turns respectively. When x, y or z are primed, it is an indication that the cube must be rotated in the opposite direction. When they are squared, the cube must be rotated 180 degrees.
The most common deviation from Singmaster notation, and in fact the current official standard, is to use "w", for "wide", instead of lowercase letters to represent moves of two layers; thus, a move of Rw is equivalent to one of r.
For methods using middle-layer turns (particularly corners-first methods) there is a generally accepted "MES" extension to the notation where letters M, E, and S denote middle layer turns. It was used e.g. in Marc Waterman's Algorithm.
M (Middle): the layer between L and R, turn direction as L (top-down)
E (Equator): the layer between U and D, turn direction as D (left-right)
S (Standing): the layer between F and B, turn direction as F
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (f b u d l r) refer to the inner portions of the cube (called slices). An asterisk (L*), a number in front of it (2L), or two layers in parenthesis (Ll), means to turn the two layers at the same time (both the inner and the outer left faces) For example: (Rr)' l2 f' means to turn the two rightmost layers counterclockwise, then the left inner layer twice, and then the inner front layer counterclockwise. By extension, for cubes of 6x6 and larger, moves of three layers are notated by the number 3, for example 3L.
An alternative notation, Wolstenholme notation, is designed to make memorizing sequences of moves easier for novices. This notation uses the same letters for faces except it replaces U with T (top), so that all are consonants. The key difference is the use of the vowels O, A and I for clockwise, counterclockwise and 180-degree turns, which results in word-like sequences such as LOTA RATO LATA ROTI (equivalent to LU′R′UL′U′RU2 in Singmaster notation). Addition of a C implies rotation of the entire cube, so ROC is the clockwise rotation of the cube around its right face.
Rubik's Cube software
Puzzles like the Rubik's Cube can be simulated by computer software, which provide functions such as recording of player metrics, storing scrambled Cube positions, conducting online competitions, analyzing of move sequences, and converting between different move notations. Software can also simulate very large puzzles that are impractical to build, such as 100×100×100 and 1,000×1,000×1,000 cubes, as well as virtual puzzles that cannot be physically built, such as 4- and 5-dimensional analogues of the cube.

 Posted in:
Posted in: 
 Follow Us on Twitter!
Follow Us on Twitter!









